
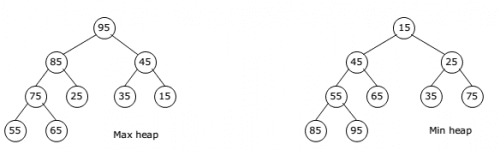
Insert the new element at the end of the tree.įor Min Heap, the above algorithm is modified so that parentNode is always smaller than newNode.Īlgorithm for deletion in Max Heap If nodeToBeDeleted is the leafNodeĮlse swap nodeToBeDeleted with the lastLeafNodeįor Min Heap, above algorithm is modified so that both childNodes are greater smaller than currentNode.Insert the newNode at the end (last node from left to right.) Loop from the first index of non-leaf node down to zeroįor Min-Heap, both leftChild and rightChild must be larger than the parent for all nodes.Īlgorithm for insertion in Max Heap If there is no node, To create a Max-Heap: MaxHeap(array, size) Repeat steps 3-7 until the subtrees are also heapified.Swap largest with currentElement Swap if necessary.If rightChild is greater than element in largest, set rightChildIndex as largest. element at ith index), set leftChildIndex as largest. If leftChild is greater than currentElement (i.e. Min Heap and Max Heap Implementation in Java Techie Delight PriorityQueue (Java Platform SE. The index of left child is given by 2i + 1 and the right child is given by 2i + 2. PriorityQueue pq new PriorityQueue() Using Java generics.To do both of these, we return root node. Start from the first index of non-leaf node whose index is given by n/2 - 1. This will return the maximum element if a max-heap is used and the minimum number if a min-heap is used.We can impose the heap-ordering restriction on any binary tree. The largest key in a heap-ordered binary tree is found at the root. Create a complete binary tree from the array A binary tree is heap-ordered if the key in each node is larger than (or equal to) the keys in that nodes two children (if any).It is used to create a Min-Heap or a Max-Heap. Heapify is the process of creating a heap data structure from a binary tree. Some of the important operations performed on a heap are described below along with their algorithms. This type of data structure is also called a binary heap. After that, we’ll implement the decrease-key operation. Next, we’ll implement the updates for the basic operations. First of all, we’ll review the usage and idea of min-heaps. This property is also called min heap property. Overview In this tutorial, we’ll present the decrease-key operation for the min heap-based priority queue. always smaller than the child node/s and the key of the root node is the smallest among all other nodes.This property is also called max heap property. always greater than its child node/s and the key of the root node is the largest among all other nodes.Heap data structure is a complete binary tree that satisfies the heap property, where any given node is Decrease Key and Delete Node Operations on a Fibonacci Heap.


 0 kommentar(er)
0 kommentar(er)
